Unlocking The Secrets Of A Area Of A Circle: Your Simple Guide To Understanding Space

By Eloisa HilpertJul 13, 2025

Have you ever stopped to think about what "area" truly means? It's a word we use a lot, in so many different ways, isn't it? Like, you might talk about a "rest area" on the highway, a "break room" at work, or even that tiny "area between the nose and the upper lip" as "My text" mentions. Or perhaps you're wondering about an "areal estimate of corn in Iowa," which "My text" also brings up, showing how "area" can describe a region, big or small. In a way, it’s all about defining a space, whether it's a physical spot or a conceptual boundary.

This idea of defining a space is actually pretty helpful when we start thinking about shapes. Just as "My text" talks about "an open area outside of a building" or "the area around a pond," we can think of the amount of flat surface inside a shape. So, when we talk about a circle, we're really just focusing on the amount of flat surface it covers. It’s that entire enclosed region, that bit of ground or paper that the circle takes up, you know? It's the measurement of the two-dimensional space that a circle occupies, which is quite a specific kind of "area" compared to some of the general uses "My text" outlines, like "a small area may also be set aside with a coffeemaker."

Today, we're going to explore this very specific kind of space: **a area of a circle**. It's a fundamental idea in math, and honestly, it pops up in more places than you might think. From designing round tables to planning gardens, understanding how much space a circle occupies is a rather useful skill. So, let's get into what makes this particular "area" special and how we figure it out, okay? It's a concept that has been puzzling and helping people for a very long time, and we'll see why it remains so important.

What Exactly is a Area of a Circle?
Why Does a Area of a Circle Matter?
The Key Players: Radius and Pi
- Understanding the Radius
- Getting to Know Pi (π)
The Simple Formula for a Area of a Circle
Putting the Formula to Work: Real-World Examples
A Little History: How We Figured Out the Area of a Circle
Common Questions About a Area of a Circle

What Exactly is a Area of a Circle?

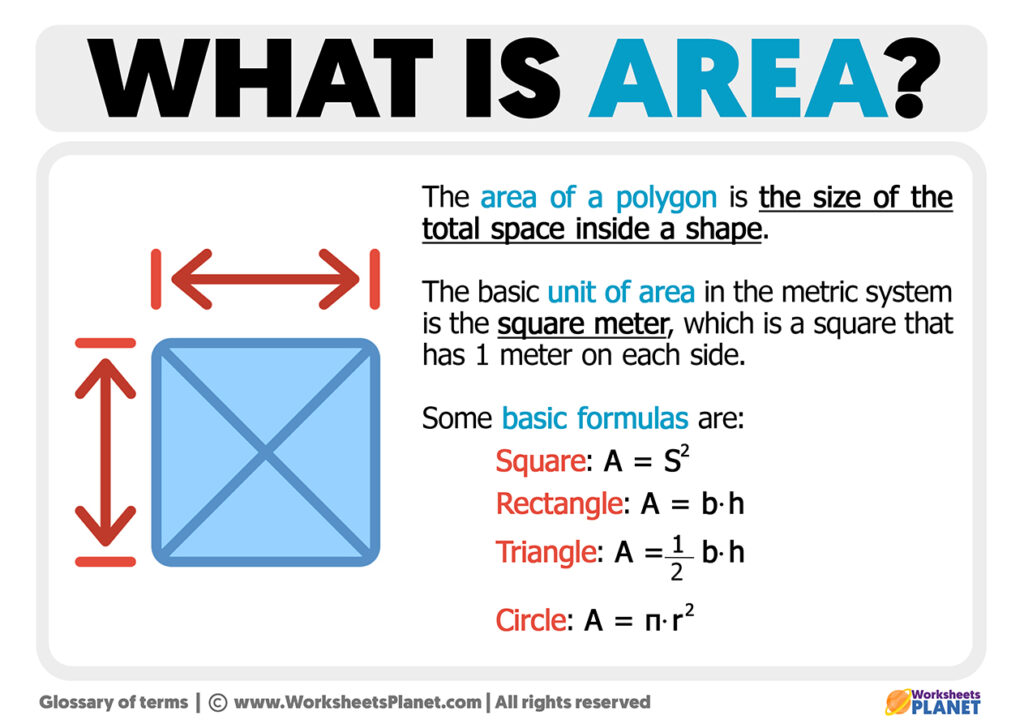
When someone mentions "a area of a circle," they are talking about the total amount of flat space enclosed within the circle's boundary. Imagine drawing a perfect circle on a piece of paper. The "area" is all the paper inside that line. It’s the two-dimensional measurement of the surface a circle covers, so it's usually measured in square units, like square inches or square meters. This is a bit different from, say, the "area circled in figure 2" that "My text" refers to, which might be a specific part of an image, or "the area people can walk on" as a footpath. Here, we're talking about the entire, continuous space of the whole circle, you know?

Think of it like this: if you wanted to cover a circular patch of ground with grass, the area would tell you how much grass seed you need. It's the "stuff" inside the shape. This concept is pretty much the same for any shape, whether it's a square, a triangle, or a circle. It’s always about the space it occupies on a flat surface, basically. We are looking at the entire region, not just a specific point or a line, which is what makes it a measurement of "area."

To put it another way, if you could cut out the circle from the paper, the area is the size of that piece you cut out. It's the amount of surface contained within the circular boundary. This measurement is always expressed in square units because it accounts for both length and width, even though a circle doesn't have straight sides in the usual sense. So, it's not just a length, but a measurement of the spread-out space, which is rather important.

Why Does a Area of a Circle Matter?

Knowing how to find a area of a circle is surprisingly useful in daily life, and not just for math homework. For instance, if you’re planning a circular garden bed, you’d need to know its area to buy the right amount of soil or mulch. Or, if you’re making a round pizza, the area helps you figure out how much dough you need. It’s a pretty practical piece of information, really, and saves you from guessing or wasting materials.

Beyond simple tasks, this measurement is crucial in many fields. Engineers use it when designing pipes or tunnels, as the cross-sectional area affects flow. Architects consider it for circular rooms or domes, understanding how much floor space is available. Even in art, understanding area helps artists plan their compositions on circular canvases or design round mosaics. So, it's not just some abstract math concept; it has real-world applications that influence how things are built and designed, you see.

Consider a situation where you're trying to figure out how much paint you need for a circular wall decoration. Knowing the area means you can buy just the right amount, avoiding extra cans or multiple trips to the store. Similarly, if you're installing a circular rug, the area tells you exactly how much floor it will cover. It's a fundamental measurement that allows for planning and precision in so many different projects, which is pretty neat when you think about it.

The Key Players: Radius and Pi

To figure out a area of a circle, we only need two main pieces of information: the radius and a special number called Pi. These two elements are absolutely central to the calculation, and honestly, you can't get the area without them. They are like the essential ingredients in a recipe, so to speak, each playing a very specific role in the process.

Understanding the Radius

The radius of a circle is simply the distance from its very center to any point on its edge. Imagine a string tied to the middle of a circle; if you pull that string taut to the edge, the length of the string is the radius. It's half of the circle's diameter, which is the distance straight across the circle through its center. So, if you know the diameter, you just divide it by two to get the radius. It's pretty straightforward, actually, and often the easiest measurement to get.

Knowing the radius is key because it defines the size of the circle. A larger radius means a bigger circle, and thus, a larger area. It makes sense, doesn't it? The further out you go from the center, the more space the circle covers. This measurement is often represented by the letter 'r' in formulas, and it’s always a positive number because it represents a real distance. You can't have a circle with a zero or negative radius, after all.

To visualize the radius, picture a bicycle wheel. The spokes extending from the center hub to the outer rim are all examples of radii. Each spoke is the same length, showing how the radius is consistent from the center to any point on the circle's boundary. This consistent distance is what gives the circle its perfectly round shape, and it's the foundation for calculating its enclosed space, you know?

Getting to Know Pi (π)

Pi, symbolized by the Greek letter π, is one of the most famous numbers in mathematics. It's a constant, meaning its value never changes, and it's approximately 3.14159. What's really cool about Pi is that it represents the ratio of a circle's circumference (the distance around it) to its diameter. No matter how big or small a circle is, if you divide its circumference by its diameter, you'll always get Pi. It's rather consistent, you know, across all circles in the universe.

Pi is an irrational number, which means its decimal representation goes on forever without repeating. For most everyday calculations, using 3.14 or 3.14159 is accurate enough. Sometimes, for very precise engineering or scientific work, many more decimal places are used, but for general purposes, a few digits work well. It's a fundamental constant that connects the dimensions of all circles, and honestly, it’s a pretty amazing concept once you think about it. You can learn more about Pi on other sites, too, as its history is quite rich.

How to Find the Area of an Octagon in 3 Easy Steps — Mashup Math

Area of a Rectangle - Math Steps, Examples & Questions

Detail Author 👤:

Name : Eloisa Hilpert
Username : tstark
Email : jamey50@hotmail.com
Birthdate : 1997-03-24
Address : 9201 Kaitlin View North Freida, OR 18460-7200
Phone : +1-610-210-8849
Company : Yost-Kuvalis
Job : ccc
Bio : Velit et aliquam et id consequatur reprehenderit culpa. Ullam aut qui impedit quia dolores ut neque iusto. Qui quibusdam debitis beatae ut vel error nostrum. Facere architecto expedita vel.

Socials 🌐

linkedin:

url : https://linkedin.com/in/kaden_dev
username : kaden_dev
bio : Incidunt aut ipsam impedit et vel.
followers : 1733
following : 932

instagram:

url : https://instagram.com/luettgenk
username : luettgenk
bio : Qui ab consequatur quod ut velit. Sit soluta delectus nihil ullam autem.
followers : 840
following : 1961

twitter:

url : https://twitter.com/kaden.luettgen
username : kaden.luettgen
bio : Doloribus et hic praesentium. Consectetur facilis dolores cupiditate. Et molestias ea minus harum. Voluptas dolorem eaque repudiandae sint et eius amet fugiat.
followers : 1546
following : 2988

facebook:

url : https://facebook.com/kaden_dev
username : kaden_dev
bio : Earum harum in repellendus nihil corrupti quibusdam. Hic autem ab quo.
followers : 1820
following : 1285